Table of Contents
Ce guide présente les notions de base du calcul vectoriel et montre comment manipuler et visualiser des vecteurs en Python à l’aide de NumPy et Matplotlib, avec des exemples concrets et des illustrations pratiques pour un public débutant en France.
Principes et opérations élémentaires sur les vecteurs
Un vecteur est un objet mathématique défini par des composantes suivant les axes d’un repère : dans le plan, un vecteur u se représente par (ux, uy), et dans l’espace par (ux, uy, uz). Les opérations usuelles sont l’addition composante par composante, la multiplication par un scalaire, le produit scalaire et le calcul de la norme.
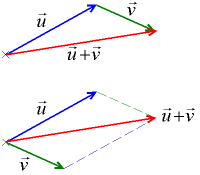
L’addition de deux vecteurs u = (ux, uy) et v = (vx, vy) donne u + v = (ux + vx, uy + vy). La multiplication par un scalaire s traduit par s·u = (s·ux, s·uy). Le produit scalaire u·v vaut uxvx + uyvy, et la norme ||u|| = √(u·u) = √(ux2 + uy2).
Le barycentre G de n points A₁,…,Aₙ de pondérations a₁,…,aₙ vérifie ∑ aᵢ·→GAᵢ = →0 ; si tous les coefficients sont égaux (isobarycentre), →OG = (1/n)∑ →OAᵢ. Le centre de masse d’un ensemble de points pondérés coïncide avec le barycentre correspondant.
Manipuler le calcul vectoriel avec NumPy et Matplotlib
NumPy représente un vecteur par un tableau 1D (numpy.array). Par exemple, u = np.array([3, 2]) définit le vecteur (3, 2). Matplotlib permet de tracer ces vecteurs graphiquement, notamment avec pyplot.quiver() pour dessiner des flèches dans un repère cartésien.
Représentation et tracé d’un vecteur
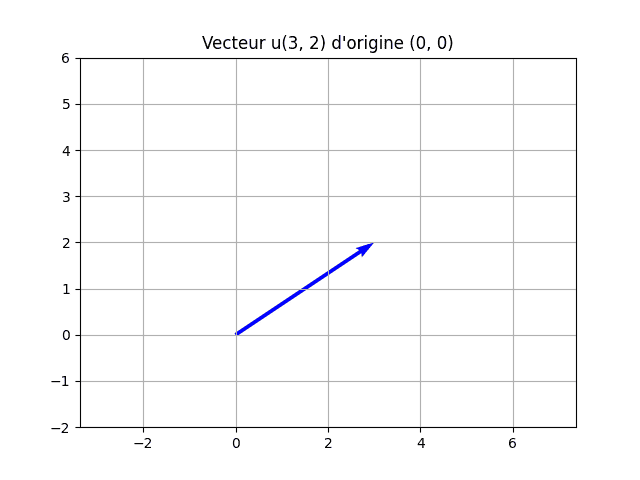
Avec Matplotlib, on peut tracer un vecteur d’origine (0,0) et de composantes (3, 2) ainsi :
plt.quiver(0, 0, 3, 2, color=’b’, angles=’xy’, scale_units=’xy’, scale=1)
Addition et multiplication par un scalaire
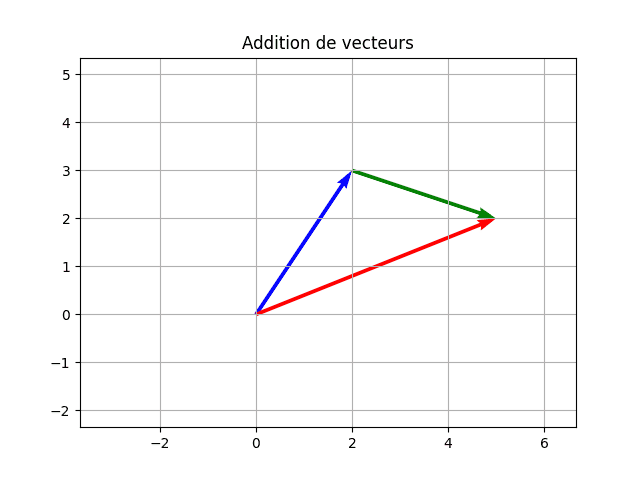
Dans NumPy, l’addition se fait composante par composante : u = np.array([2,3]); v = np.array([3,-1]); u+v donne array([5, 2]). Le tracé peut montrer u en bleu, v en vert (déplacé) et w = u+v en rouge.
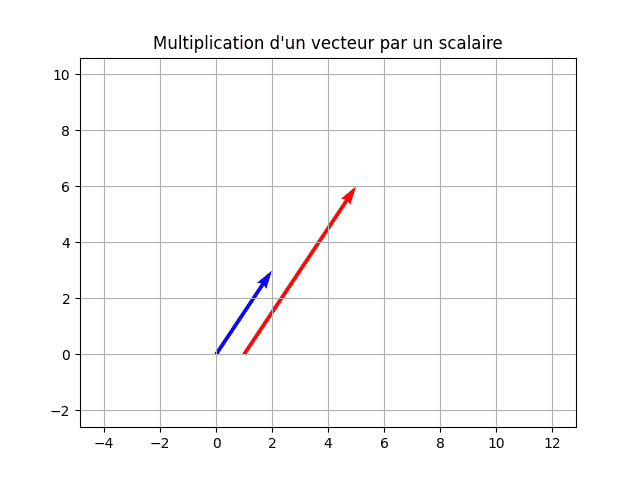
La multiplication par un scalaire est directe : 2*u renvoie array([4, 6]).
Produit scalaire et norme
Le produit scalaire s’obtient avec np.dot(u, v). Exemple : u = np.array([1, 2]), v = np.array([3, 4]) ; np.dot(u, v) retourne 11 (1×3 + 2×4). La norme se calcule avec np.linalg.norm(u) : u = [3,4] donne 5.
Application de fonctions et vectorisation
NumPy applique une fonction à l’ensemble des composantes sans boucle explicite : u = np.array([4, 9, 16, 25]); np.sqrt(u) renvoie array([2., 3., 4., 5.]). Cette vectorisation facilite la génération de figures, par exemple le cercle unité via θ = np.linspace(0, 2π, 400), x = cos(θ), y = sin(θ).
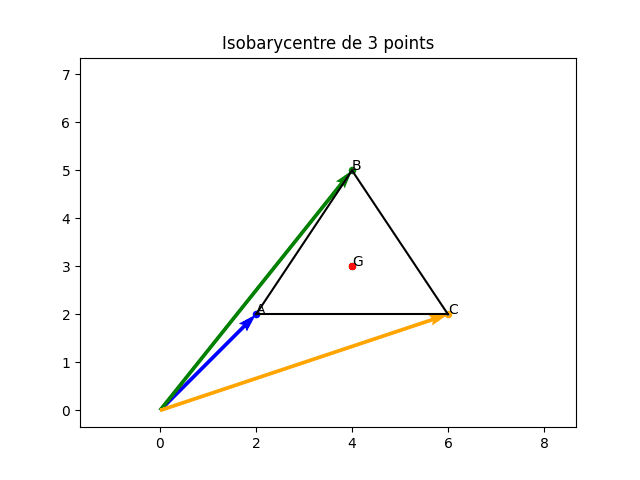
Isobarycentre de trois points et centre de masse d’un disque
Exemple numérique : pour A(2,2), B(4,5), C(6,2), on construit OA, OB, OC comme tableaux NumPy puis OG = (1/3)*(OA+OB+OC). Le script affiche :
Point A (2, 2) · Point B (4, 5) · Point C (6, 2)
Isobarycentre G (4,0, 3,0) — ce qui correspond ici au point d’intersection des médianes du triangle.
Pour vérifier que le barycentre de points uniformément répartis dans un disque coïncide avec son centre, on génère les vecteurs de position des points intérieurs au disque (test ux² + uy² ≤ r²), on calcule OG = (1/n)·∑ OA et on trace les points et OG. Dans l’exemple avec r = 1 et centre (ox, oy) = (1, 1), le calcul renvoie :
Coordonnées du point G : (1,0000000000000835, 1,0)
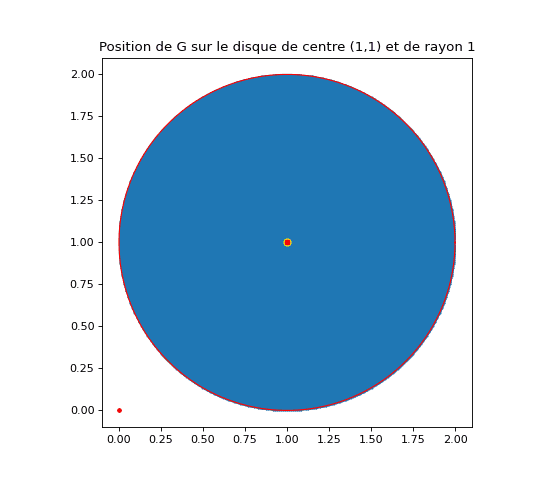
On constate que G (en rouge) coïncide visuellement avec le centre du disque (en jaune). De légers écarts peuvent apparaître si la répartition des points n’est pas parfaitement uniforme.
Exercice : centre de masse d’un demi‑disque
En appliquant la même méthode au demi‑disque supérieur (partie y ≥ 0 du disque centré en (ox, oy)), la position théorique du centre de masse vaut (ox, oy + 4r/(3π)). Pour l’exemple ox = 1, oy = 1 et r = 1, la valeur théorique est :
Centre de masse du demi‑disque : (1, 1,4244131815783876)
Le calcul numérique approché renvoie :
Coordonnées du point G : (0,99999999999634803, 1,4241421003656138)
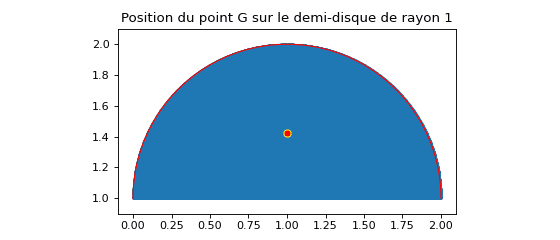
Le résultat montre une très bonne concordance entre la formule analytique et l’estimation par barycentre discret.
Perspectives et bonnes pratiques en calcul vectoriel
La combinaison NumPy + Matplotlib permet d’expérimenter rapidement avec le calcul vectoriel : représentation, opérations arithmétiques, produit scalaire, normes, application de fonctions vectorisées et calculs barycentriques. Pour des datasets volumineux, privilégier les fonctions vectorisées (meshgrid, masques booléens) pour des raisons de performance.
Les concepts présentés ici constituent des bases utiles en mathématiques appliquées, statistiques (centroïdes, k‑moyennes) et physique (forces, vitesses). Le code fourni est facilement réutilisable et modifiable pour d’autres figures géométriques ou dimensions.

